Parameterization & Surface fitting
[edit]During the reverse engineering of CAD models, free-form regions need to be approximated with trimmed tensor-product B-splines. There are many methods available for surface fitting, but all of them require an initial parameterization (flattening) of the data points, which can have a substantial effect on the quality of the final surface. While mesh parameterization has a rich literature, the specific requirements of trimmed fitting are quite different from those of texture mapping or quad meshing. Motivated by this, we worked on mesh parameterization methods that enable fitting high-quality trimmed surfaces with minimal user intervention.
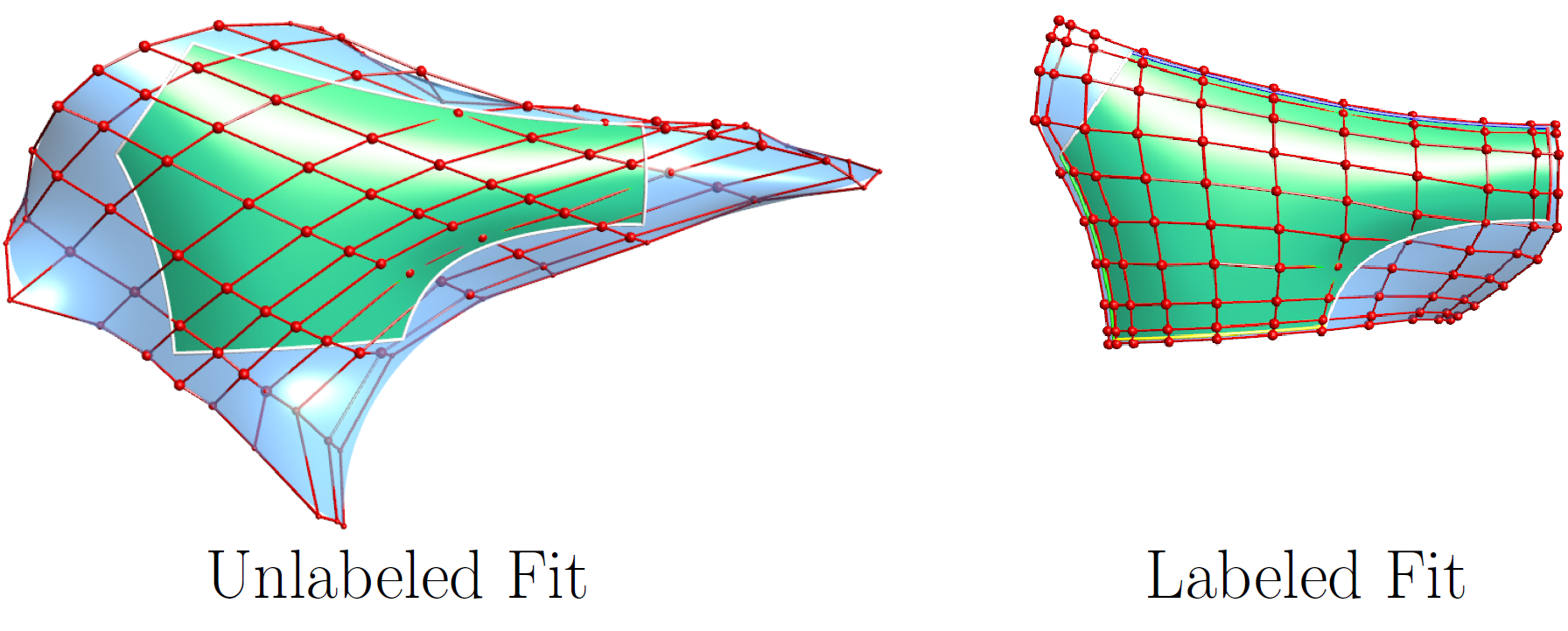
Labeled fitting
We introduced a novel technique to aid trimmed surface parameterization, called labeling. Boundary curves may have assigned labels, indicating that they belong to one of the four sides (North,East,South,West) of the domain rectangle, or represent trim curves. We utilize this labeling information to compute a constrained As-Rigid-As-Possible (ARAP) parameterization.
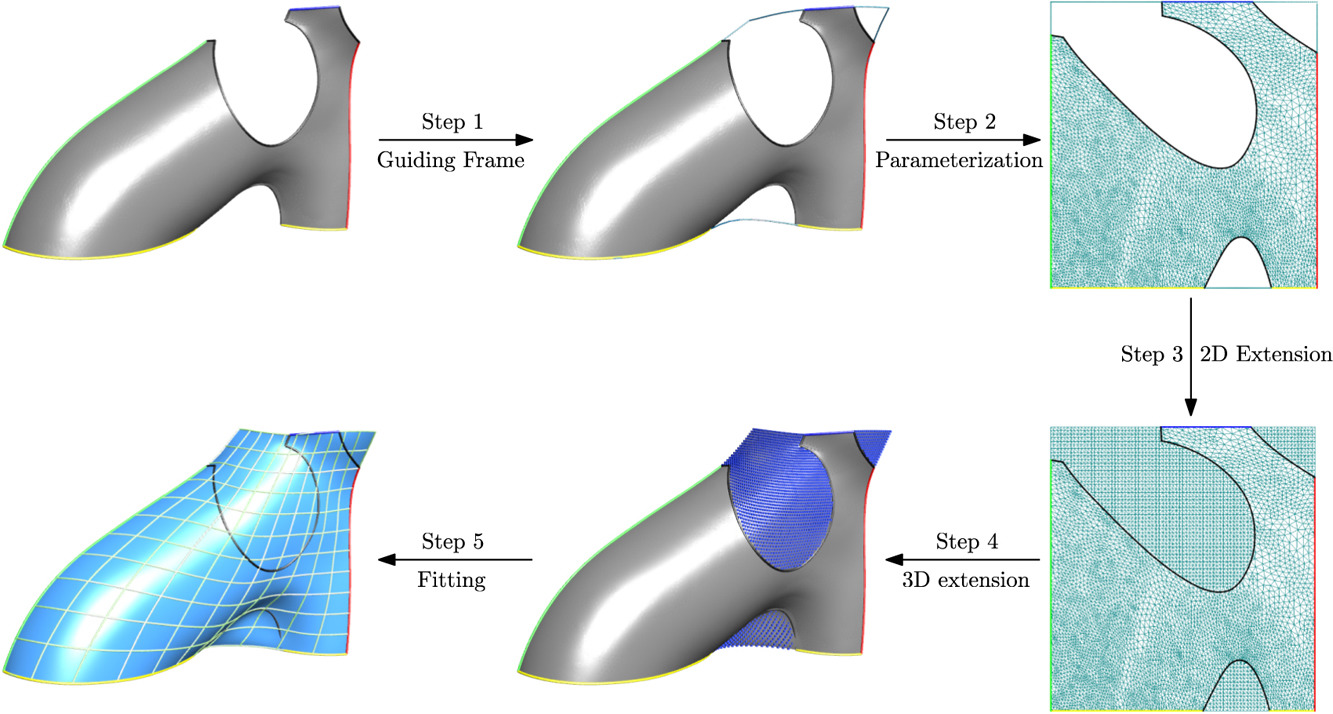
A well-known issue for trimmed fitting concerns "weak" control points with very few data points in their support, leading to numerical instabilities and wildly oscillating fits. We developed a method to stabilize trimmed fitting, by smoothly extending the surface. This technique is combined with labeling to produce very high-quality surfaces.
M. Vaitkus, T. Várady, Parameterizing and extending trimmed regions for tensor-product surface fitting. Computer-Aided Design, Vol. 104, pp. 125-140, 2018. DOI • BibTeX
M. Vaitkus, T. Várady, Mesh Extension for Labeled Surface Fitting. Proceedings of the Ninth Hungarian Conference on Computer Graphics and Geometry, pp. 1-9, 2018. Full paper • BibTeX
M. Vaitkus, T. Várady, Labeled parameterization for high-quality surface fitting. Proceedings of the Conference of the Hungarian Association for Image Processing and Pattern Recognition, pp. 675-686, 2015. Full paper • BibTeX
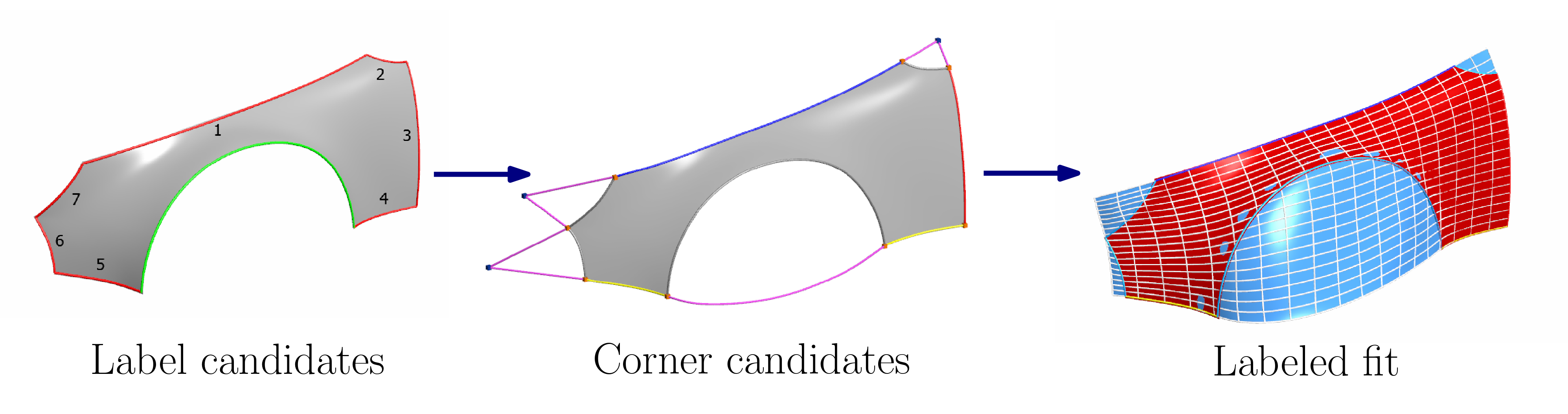
Automatic labeling
We have also developed an algorithm for the automatic assignment of labels. We developed a set of heuristics for classifying boundary curves as label candidates or trim curves, and based on these a natural label configuration is computed.
M. Vaitkus, T. Várady, A Labeling Algorithm for Trimmed Surface Fitting. Computer-Aided Design and Applications, Vol. 16, pp. 720-732, 2019. DOI • BibTeX
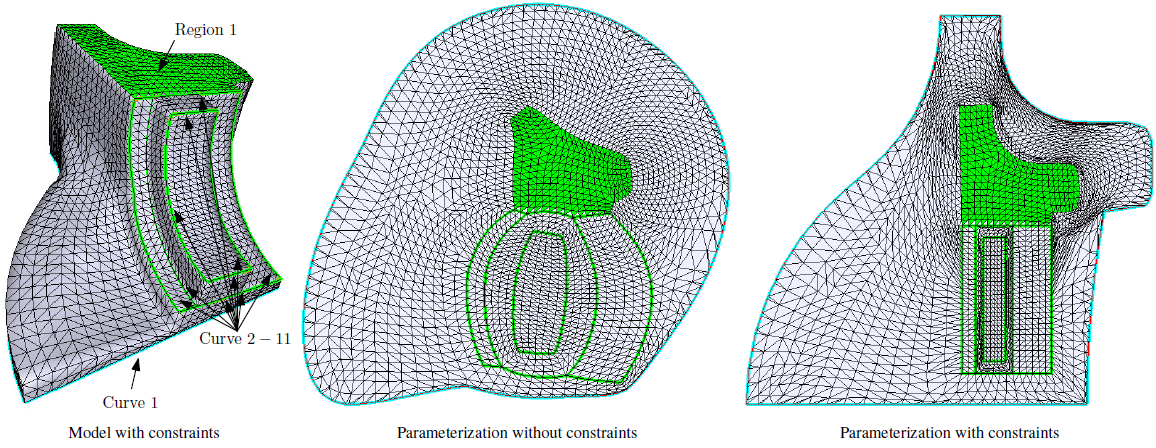
Geometric constraints
We developed a framework for mesh parameterization under general geometric constraints. We may want to request that certain curves are mapped to straight lines or circles, that lines be perpendicular or parallel or that certain regions preserve their shape after flattening. We satisfy combinations of such constraints using a variant of local-global ARAP parameterization. Labeled parameterization is a particular application of this general technique.
M. Vaitkus, T. Várady, A general framework for constrained mesh parameterization. Proceedings of the 31st Spring Conference on Computer Graphics, pp. 15-21, 2015. DOI • BibTeX
M. Vaitkus, T. Várady, Mesh Parameterization with Geometric Constraints. Proceedings of the Seventh Hungarian Conference on Computer Graphics and Geometry, pp. 37-45, 2014. Full paper • BibTeX