Control point based schemes are dominant in computer-aided design for defining free-form parametric curves and surfaces. The control points are associated with a set of basis functions that fundamentally determine the versatility of shape editing, the mathematical properties of the scheme and the computational aspects of related algorithms.

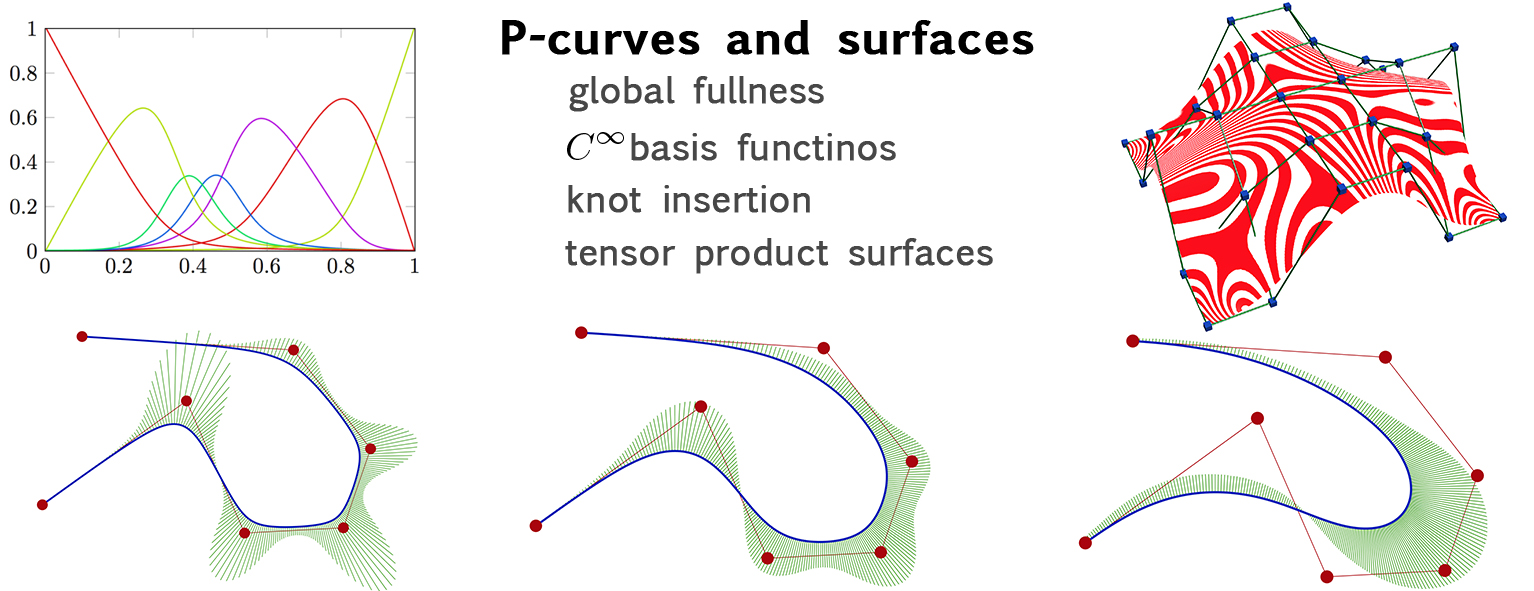
Proximity curves represent such an approach. A family of curves is constructed that depends on a proximity parameter making it possible to sweep a base curve continuously to its control polygon. The concept extends to proximity surfaces, as well. Here we deal with control point based representations; typically curves are constrained at their endpoints, surfaces along their boundaries, and the shape interiors are determined by the location of the control points in between. Proximity makes it possible to impose further constraints in addition to the positional and cross-derivative constraints, while the control polygons/polyhedra remain unchanged. Such constraints may include keeping the distances between the shape and the control structure within a certain range or limiting the radius of curvatures by a threshold.

I. Kovács, T. Várady, P-curves and surfaces: parametric design with global fullness control. Computer-Aided Design, Vol. 90, pp. 113-122, 2017. DOI • BibTeX

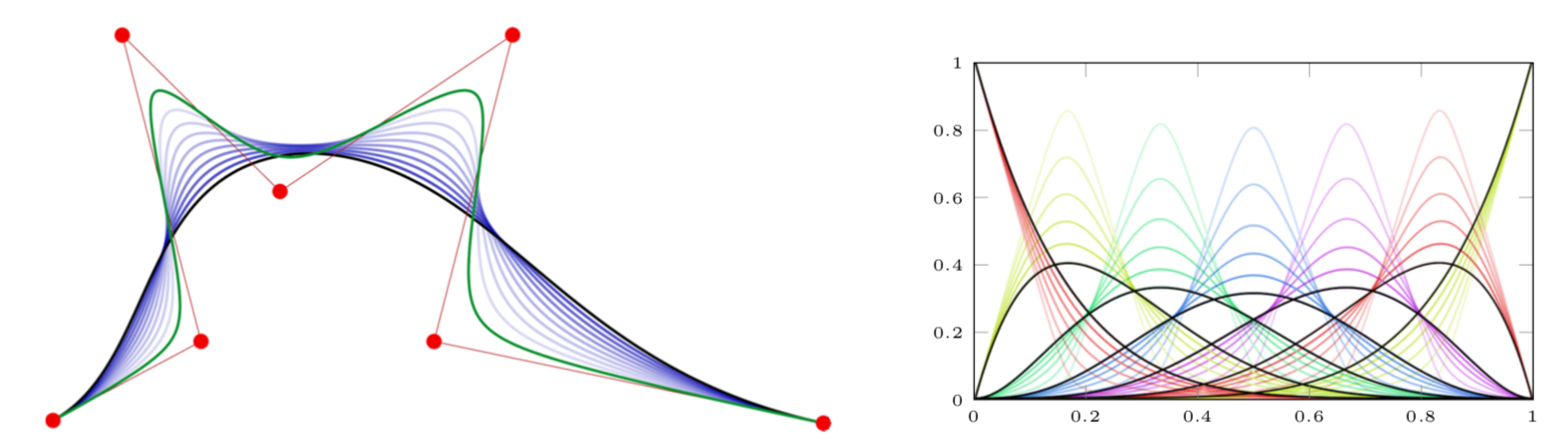
We introduced two different representations to define proximity curves. The first one, P-curve, is based on the concept of generalized barycentric coordinates, using a new sort of basis functions. The second approach is based on second-order finite differences and can reproduce classical representations like Bézier and B-spline curves, therefore I refer to them as P-Bézier and P-BSpline curves. The representations satisfy many important requirements that are useful in CAD, including positivity, convex combination, natural knot insertion and so on.

I. Kovács, T. Várady, Favorable approximating properties of the P-Bézier basis. Proceedings of the Ninth Hungarian Conference on Computer Graphics and Geometry, pp. 10-15, 2018. Full paper • BibTeX

I. Kovács, T. Várady, P-Bézier and P-Bspline curves – new representations with proximity control. Computer Aided Geometric Design, Vol. 62, pp. 117-132, 2018. DOI • BibTeX

Bézier proximity curves

A drawback of the above approach is that it uses a non-standard representation that needs to be approximated to be exported into a CAD system. We have also investigated whether proximity curves can be represented as Bézier curves of higher degree.

P. Salvi, T. Várady, Proximity by multiplicity. Proceedings of the Workshop on the Advances of Information Technology, pp. 68-73, 2022. Full paper • BibTeX

εκ-curves

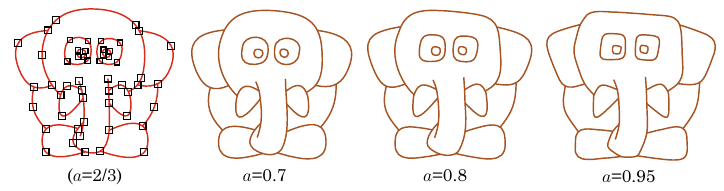
An extension of the interpolatory κ-curves, where weights can be associated with individual control points, resulting in an effect similar to proximity.

K.T. Miura, R.U. Gobithaasan, P. Salvi, D. Wang, T. Sekine, Sh. Usuki, J. Inoguchi, K. Kajiwara, εκ-curves: Controlled local curvature extrema. The Visual Computer, 2021. DOI • BibTeX

• A cubic generalization of κ-curves
• An alternative trigonometric basis
• Investigation of applicability to other bases